Suite de Fibonacci

Définition de la suite de Fibonacci :

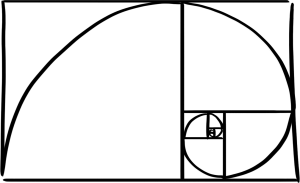
Déjà établie au 12ème siècle par Leonardo Pisano, la suite de Fibonacci (en anglais : Fibonacci Sequence) est une séquence mathématique infinie dans laquelle chaque nombre est formé par la somme des deux nombres précédents :

• 1
• 2
• 3
• 5
• 8
• 13
• 21
• etc.

Ainsi, les intervalles entre les nombres deviennent de plus en plus grands à mesure que les nombres eux-mêmes augmentent.
La suite de Fibonacci est également appelée nombre d'or ou spirale dorée, mais elle s'en distingue par la variation alternée des quotients.

Utilisation de la suite de Fibonacci :

Les équipes utilisent souvent la suite de Fibonacci lors du Planning Poker pour estimer la charge de travail. Les nombres sont relatifs et n'ont pas d'unité de mesure fixe sous-jacente. De plus, l'écart croissant avec le nombre précédent et suivant permet une bonne estimation aussi bien des très petites que des très grandes Stories.

Avantages de la suite de Fibonacci :

• Création d'une référence ou d'un standard de comparaison pour l'estimation du travail.
• Des estimations relatives plus précises.